Life in the Fast Lane
Get the code here!
Conway’s Game of Life has been an inspiration to computer scientists since it’s creation in 1970. Life is a simulation of cells arranged in a two-dimensional grid. Each cell can be in one of two states, alive or dead. I will leave the full explanation of Life to Wikipedia, and only restate here the rules regarding the interactions between cells:
- Any live cell with fewer than two live neighbors dies, as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Note that in our implementation of Life, like many others, the environment wraps around to the other side at the edges, like in Pac-Man.
This text chronicles my journey in improving the performance of a Life kernel. To make this guide representative of many problems in performance optimization for scientific kernels, I have disallowed myself from pursuing algorithmic optimizations (that said, if you haven’t seen Hashlife, it is worth checking out). Many of the optimization techniques we see here should be applicable to a wide variety of codes, and will focus on optimizing the naive algorithm for a given architecture.
These techniques can make the code go faster, but they increase code complexity by several orders of magnitude and tend to need different tunings for different machines. If someone else has written an optimized version of code that does what you want to do, I would strongly recommend using that code before trying anything you see here. The general advice is to use optimized libraries whenever possible.
reference.c
Like many logical simulations, life is fully deterministic. This means that we can determine if our simulation is correct by comparing our output to a reference implementation. The reference implementation we use will also provide a starting point for optimization. The reference implementation I use has been adapted from the RosettaCode C implementation. Rather than expound on the code for ages, I will let you read it yourself. Explanatory comments are included.
#include <stdlib.h>
unsigned *reference_life (const unsigned height,
const unsigned width,
const unsigned *initial,
const unsigned iters) {
//"universe" is the current game of life grid. We will store "alive" as a 1
//and "dead" as a 0.
unsigned *universe = (unsigned*)malloc(sizeof(unsigned) * height * width);
//"new" is a scratch array to store the next iteration as it is calculated.
unsigned *new = (unsigned*)malloc(sizeof(unsigned) * height * width);
//We must load the initial configuration into the universe memory.
for (unsigned y = 0; y < height; y++) {
for (unsigned x = 0; x < width; x++) {
universe[y * width + x] = initial[y * width + x];
}
}
//The main loop: a likely target for later optimization.
for (unsigned i = 0; i < iters; i++) {
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++) {
//Here we loop over the neighbors and count how many are alive.
unsigned n = 0;
for (int yy = y - 1; yy <= y + 1; yy++) {
for (int xx = x - 1; xx <= x + 1; xx++) {
//This is a redundant way to perform this operation. Since "alive"
//is represented as 1 and "dead" is represented as 0, we can just
//add universe[...] to n without the conditional branch.
if (universe[((yy + height) % height) * width
+ ((xx + width) % width)]) {
n++;
}
}
}
//This statement is to avoid counting a cell as a neighbor of itself.
if (universe[y * width + x]) {
n--;
}
//This fairly tight logic determines the status of the cell in the next
//iteration. We have to store this in a new array to avoid modifying
//the original array as we calculate the new one.
new[y * width + x] = (n == 3 || (n == 2 && universe[y * width + x]));
}
}
//These loops copy the new state array into the current state array,
//completing an iteration.
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++) {
universe[y * width + x] = new[y * width + x];
}
}
}
free(new);
return universe;
}This reference implementation is easy to read and understand, but it is pretty slow. It has lots of conditional and arithmetic logic in the inner loop and it copies the entire universe at every step. The reference code is our starting point, and we will use it to check the correctness of our optimized versions.
bench.c
Before we start optimizing, lets write our benchmarking and test code. Having an accurate benchmark that tests a common case for our code gives us the information we’ll need to make optimization decisions. Our benchmark code includes test code as well. Rather than paste the whole file, I only include the highlights here.
//Return time time of day as a double-precision floating point value.
double wall_time (void) {
struct timeval t;
//It is important to use an timer with good resolution. Many common functions
//that return the time are not precise enough for timing code. Since timers
//are typically system-specific, research timers for your system. I have
//found that omp_get_wtime() is usually quite good and is available
//everywhere there is OpenMP.
gettimeofday(&t, NULL);
return 1.0*t.tv_sec + 1.0e-6*t.tv_usec;
}Note that in our benchmark, TIMEOUT is set to 0.1 seconds
double test_time = 0;
unsigned *test;
//We must run the benchmarking application for a sufficient length of time to
//avoid variations in processing speed. We do this by running an increasing
//number of trials until it takes at least TIMEOUT seconds.
for (trials = 1; test_time < TIMEOUT; trials *= 2) {
//Unless we want to measure the cache warm-up time, it is usually a good
//idea to run the problem for one iteration first to load the problem
//into cache.
test = life(height, width, initial, 1);
free(test);
//Benchmark "trials" runs of life.
test_time = -wall_time();
for (int i = 0; i < trials - 1; ++i){
test = life(height, width, initial, iters);
free(test);
}
test = life(height, width, initial, iters);
test_time += wall_time();
}
trials /= 2;
test_time /= trials;simple.c
Before we complicate the reference implementation with our optimizations, let’s simplify it a little bit. Here is the new inner loop:
for (unsigned i = 0; i < iters; i ++) {
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++) {
unsigned n = 0;
for (int yy = y - 1; yy <= y + 1; yy++) {
for (int xx = x - 1; xx <= x + 1; xx++) {
//Directly add "universe" values to "n"
n += universe[((yy + height) % height) * width
+ ((xx + width) % width)];
}
}
n -= universe[y * width + x];
new[y * width + x] = (n == 3 || (n == 2 && universe[y * width + x]));
}
}
//Instead of copying "new" into universe every time, just swap the pointers
unsigned *tmp = universe;
universe = new;
new = tmp;
}On a 8192x8192 grid for 256 iterations, these optimizations provide a 1.288x speedup over the reference implementation. Not much, but we are just getting started!
Environment
Typically, programs perform differently on different platforms and with different compilers and flags. For the record, I am using gcc version 4.9.3 with the compiler flags “-O3 -march=native”. Meet my processor! Here’s the output of the command lscpu on my machine.
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Byte Order: Little Endian
CPU(s): 40
On-line CPU(s) list: 0-39
Thread(s) per core: 2
Core(s) per socket: 10
Socket(s): 2
NUMA node(s): 2
Vendor ID: GenuineIntel
CPU family: 6
Model: 63
Model name: Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHz
Stepping: 2
CPU MHz: 2600.000
BogoMIPS: 5209.96
Virtualization: VT-x
L1d cache: 32K
L1i cache: 32K
L2 cache: 256K
L3 cache: 25600K
NUMA node0 CPU(s): 0-9,20-29
NUMA node1 CPU(s): 10-19,30-39
This processor has 20 CPUs across two NUMA domains, so we’ll need to be mindful of the way that we access memory. We’ll also need to write parallel code to take advantage of our multiple CPUs.
One last thing before we jump down this rabbit hole. We need to know the peak performance so that we know when to stop! Notice that there are 12 necessary integer operations in our inner loop (we count the comparisons to 2 and 3, and we don’t count the redundant add and subtract of the cell value itself). Assume that we can do one instruction per clock cycle. The processor runs at 2.6109 clock cycles per second, and this machine supports AVX2, so we can operate on 32 8-bit sized integers at once, and there are 20 cores. Therefore, on average we can advance one cell one iteration in 7.210-12 seconds. Therefore, the theoretical peak time to compute our 8192x8192 test problem over 256 iterations is 1.24*10-1 seconds. Don’t forget it or you’ll never stop optimizing!
padding.c
Since our program is so simple, we can be pretty sure where it spends most of it’s time. Our inner loop includes complicated modular arithmetic on indices and a doubly-nested for loop. Let’s fix this! We can use a technique called “padding”. In short, instead of looking to the other side of the universe to wrap around in the inner loop, we will allocate an array with extra cells on all sides (“ghost cells”) and fill these cells with values from the other side of the array. That way, when the inner loop accesses beyond the the edges of the universe, it looks like the universe is wrapping around (and we don’t need to check to see if we are falling off the edge).
Each time we perform an iteration, the outer layer of valid ghost cells becomes invalid (we did not calculate anything on the outermost layer of the array, and this error propagates inward by one cell each iteration). To avoid copying with every iteration, we can pad with multiple ghost cell layers at once, and then run several iterations before each copy.
Note that this code assumes that width is a multiple of sizeof(unsigned).
#include <stdlib.h>
#include <stdint.h>
#define WORD sizeof(unsigned)
//OUT_GHOST is the width of the valid ghost cells after copying IN_GHOST ghost
//cell values to the border and then executing one iteration. The kernel will
//copy IN_GHOST ghost cells, then run IN_GHOST iterations before copying ghost
//cells again. OUT_GHOST can be any value greater than or equal to 0.
#define OUT_GHOST 0
#define IN_GHOST (OUT_GHOST + 1)
#define X_IN_GHOST ((OUT_GHOST/WORD + 1) * WORD)
#define Y_IN_GHOST IN_GHOST
#define X_IN_GHOST_WORDS (X_IN_GHOST/WORD)
//There are platform specific aligned malloc implementations, but it is
//instructive to see one written out explicitly. Allocates memory, then rounds
//it to a multiple of WORD. Stores a pointer to the original memory to free it.
void *aligned_malloc(int size) {
char *mem = malloc(sizeof(void*) + size + WORD - 1);
void **ptr = (void**)(((uintptr_t)(mem + sizeof(void*) + WORD - 1)) & ~((uintptr_t)(WORD - 1)));
ptr[-1] = mem;
return ptr;
}
void aligned_free(void *ptr) {
free(((void**)ptr)[-1]);
}
unsigned *life (const unsigned height,
const unsigned width,
const unsigned * const initial,
const unsigned iters) {
//Padding makes things ridiculously complicated. These constant values
//make life a little easier.
const unsigned padded_height = height + 2 * Y_IN_GHOST;
const unsigned padded_width = width + 2 * X_IN_GHOST;
const unsigned width_words = width/WORD;
const unsigned padded_width_words = padded_width/WORD;
//Oh! The careful reader will notice that I am allocating an array of
//byte-size ints! In addition to preparing us for vectorization later, this
//also reduces memory traffic.
//Also, this memory is aligned. Aligned memory access is typically faster
//that unaligned. To keep the memory aligned on each row, we have to pad
//to a multiple of the word size. We also assume the input matrix has a width
//that is a multiple of the word size.
uint8_t *universe = (uint8_t*)aligned_malloc(padded_height * padded_width);
uint8_t *new = (uint8_t*)aligned_malloc(padded_height * padded_width);
//Pack unsigned into the padded working array of uint8_t.
for (unsigned y = Y_IN_GHOST; y < height + Y_IN_GHOST; y++) {
for (unsigned x = X_IN_GHOST; x < width + X_IN_GHOST; x++) {
universe[(y * padded_width) + x] = initial[(y - Y_IN_GHOST) * width + x - X_IN_GHOST];
}
}
for (unsigned i = 0; i < iters; i += IN_GHOST) {
//Copy the ghost cells once every IN_GHOST iterations. I have not only
//simplified much of the logic (no more mod operations!), I have also
//reduced the number of instructions necessary to copy by casting the
//uint8_t array to unsigned and working with these larger values of a size
//the system is used to working with.
unsigned *universe_words = (unsigned*)universe;
for (unsigned y = 0; y < padded_height; y++) {
if (y < Y_IN_GHOST) {
//Top left
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y + height) * padded_width_words + x + width_words];
}
//Top middle
for (unsigned x = X_IN_GHOST_WORDS; x < width_words + X_IN_GHOST_WORDS; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y + height) * padded_width_words + x];
}
//Top right
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y + height) * padded_width_words + x - width_words];
}
} else if (y < height + Y_IN_GHOST) {
//Middle left
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
universe_words[y * padded_width_words + x] = universe_words[y * padded_width_words + x + width_words];
}
//Middle right
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
universe_words[y * padded_width_words + x] = universe_words[y * padded_width_words + x - width_words];
}
} else {
//Bottom left
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y - height) * padded_width_words + x + width_words];
}
//Bottom middle
for (unsigned x = X_IN_GHOST_WORDS; x < width_words + X_IN_GHOST_WORDS; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y - height) * padded_width_words + x];
}
//Bottom right
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
universe_words[y * padded_width_words + x] = universe_words[(y - height) * padded_width_words + x - width_words];
}
}
}
//The valid ghost zone shrinks by one with each iteration.
for (unsigned j = 0; j < IN_GHOST && i + j < iters; j++) {
for (unsigned y = (Y_IN_GHOST - OUT_GHOST); y < height + Y_IN_GHOST + OUT_GHOST; y++) {
for (unsigned x = (X_IN_GHOST - OUT_GHOST); x < width + X_IN_GHOST + OUT_GHOST; x++) {
//The inner loop gets much simpler when you pad the array, doesn't it?
//This is the main reason people pad their arrays before computation.
unsigned n = 0;
uint8_t *u = universe + (y - 1) * padded_width + x - 1;
//Note that constant offsets into memory are faster.
n += u[0];
n += u[1];
n += u[2];
u += padded_width;
n += u[0];
unsigned alive = u[1];
n += u[2];
u += padded_width;
n += u[0];
n += u[1];
n += u[2];
new[y * padded_width + x] = (n == 3 || (n == 2 && alive));
}
}
uint8_t *tmp = universe;
universe = new;
new = tmp;
}
}
//Unpack uint8_t into output array of unsigned.
unsigned *out = (unsigned*)malloc(sizeof(unsigned) * height * width);
for (unsigned y = Y_IN_GHOST; y < height + Y_IN_GHOST; y++) {
for (unsigned x = X_IN_GHOST; x < width + X_IN_GHOST; x++) {
out[(y - Y_IN_GHOST) * width + x - X_IN_GHOST] = universe[(y * padded_width) + x];
}
}
aligned_free(new);
aligned_free(universe);
return out;
}On a 8192x8192 grid for 256 iterations, this code achieves our first significant speedup of 5.201x over the reference version!
blocked.c
Our calculation progress linearly across each row, accessing only the rows above and below it. Life needs to access each element nine times (eight times while counting among neighbors, and once to calculate the cell itself). As computation proceeds row by row, these accesses occur in groups of three (once group for each row), and if three rows of the matrix can fit in L1 cache, then the data is only loaded once from cache per iteration. However, if our computation were more data intensive, it might benefit from a technique called blocking.
Blocking is the practice of restructuring the computation so that data in registers cache is reused before it is evicted from these locations. This keeps the relevant data for a computation in the higher (faster) levels of the memory hierarchy. Register blocking involves rewriting the inner loop of your code to reuse values you have loaded from memory instead of loading them multiple times. Cache blocking involves restructuring the ordering of loops so that the same or nearby values are accessed soon after each other. Typically, we size the cache blocks so that the entire computation fills the L1 cache.
It doesn’t help much in this case (our kernel spends more time computing than loading from memory), here’s an example of how to restructure the padded inner loop for cache blocking:
#define X_BLOCK WORD * 256
#define Y_BLOCK 256 for (unsigned j = 0; j < IN_GHOST && i + j < iters; j++) {
//Now the outer loops progress block by block.
for (unsigned y = (Y_IN_GHOST - OUT_GHOST); y < height + Y_IN_GHOST + OUT_GHOST; y += Y_BLOCK) {
for (unsigned x = (X_IN_GHOST - OUT_GHOST); x < width + X_IN_GHOST + OUT_GHOST; x += X_BLOCK) {
//The inner loops progress one by one.
for (unsigned yy = y; yy < y + Y_BLOCK && yy < height + Y_IN_GHOST + OUT_GHOST; yy++) {
for (unsigned xx = x; xx < x + X_BLOCK && xx < width + X_IN_GHOST + OUT_GHOST; xx++) {
unsigned n = 0;
uint8_t *u = universe + (yy - 1) * padded_width + xx - 1;
n += u[0];
n += u[1];
n += u[2];
u += padded_width;
n += u[0];
unsigned alive = u[1];
n += u[2];
u += padded_width;
n += u[0];
n += u[1];
n += u[2];
new[yy * padded_width + xx] = (n == 3 || (n == 2 && alive));
}
}
}
}
uint8_t *tmp = universe;
universe = new;
new = tmp;
}sse2.c
Let’s cram more operations into the inner loop using vectorization. Intel’s SSE vector intrinsics are 128 bits wide, so we can cram 16 uint8_t types into a single vector register, and operate on them all at once. To keep the code nice, we require that the width of the input is a multiple of 16. A good resource for Intel vector intrinsics is the Intel Intrinsics Guide. The best way for me to show you what the inner loop looks like at this point would be to write it out:
#define WORD (128/8) for (unsigned i = 0; i < iters; i+= IN_GHOST) {
//Because we assume the width is a multiple of the size of a SSE register,
//we can use aligned loads and stores.
__m128i *universe_words = (__m128i*)universe;
for (unsigned y = 0; y < padded_height; y++) {
if (y < Y_IN_GHOST) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y + height) * padded_width_words + x + width_words));
}
for (unsigned x = X_IN_GHOST_WORDS; x < width_words + X_IN_GHOST_WORDS; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y + height) * padded_width_words + x));
}
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y + height) * padded_width_words + x - width_words));
}
} else if (y < height + Y_IN_GHOST) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + y * padded_width_words + x + width_words));
}
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + y * padded_width_words + x - width_words));
}
} else {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y - height) * padded_width_words + x + width_words));
}
for (unsigned x = X_IN_GHOST_WORDS; x < width_words + X_IN_GHOST_WORDS; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y - height) * padded_width_words + x));
}
for (unsigned x = width_words + X_IN_GHOST_WORDS ; x < padded_width_words; x++) {
_mm_store_si128(universe_words + y * padded_width_words + x,
_mm_load_si128(universe_words + (y - height) * padded_width_words + x - width_words));
}
}
}
for (unsigned j = 0; j < IN_GHOST & j + i < iters; j++) {
//Set up a vector of ones
const __m128i ones = _mm_set_epi8(1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1);
//Set up a vector of twos
const __m128i twos = _mm_slli_epi32(ones, 1);
//Set up a vector of threes
const __m128i threes = _mm_or_si128(ones, twos);
for (unsigned y = (Y_IN_GHOST - Y_OUT_GHOST); y < height + Y_IN_GHOST + Y_OUT_GHOST; y++) {
for (unsigned x = (X_IN_GHOST - X_OUT_GHOST); x + WORD <= width + X_IN_GHOST + X_OUT_GHOST; x += WORD) {
__m128i n;
__m128i alive;
uint8_t *u = universe + (y - 1) * padded_width + x - 1;
//This is an unaligned load
n = _mm_lddqu_si128((__m128i*)u);
n = _mm_add_epi8(_mm_load_si128((__m128i*)(u + 1)), n);
n = _mm_add_epi8(_mm_lddqu_si128((__m128i*)(u + 2)), n);
u += padded_width;
n = _mm_add_epi8(_mm_lddqu_si128((__m128i*)u), n);
//This is an aligned load
alive = _mm_load_si128((__m128i*)(u + 1));
n = _mm_add_epi8(_mm_lddqu_si128((__m128i*)(u + 2)), n);
u += padded_width;
n = _mm_add_epi8(_mm_lddqu_si128((__m128i*)u), n);
n = _mm_add_epi8(_mm_load_si128((__m128i*)(u + 1)), n);
n = _mm_add_epi8(_mm_lddqu_si128((__m128i*)(u + 2)), n);
//The operation we are performing here is the same, but it looks
//very different when written in SIMD instructions
_mm_store_si128((__m128i*)(new + y * padded_width + x),
_mm_or_si128(
//We need to and with the ones vector here because the result of
//comparison is either 0xFF or 0, and we need 1 or 0.
_mm_and_si128(ones, _mm_cmpeq_epi8(n, threes)),
_mm_and_si128(alive, _mm_cmpeq_epi8(n, twos))));
}
}
uint8_t *tmp = universe;
universe = new;
new = tmp;
}
}This code achieves a speedup of 58.06x over the reference on the 8192x8192 grid for 256 iterations. Not bad.
avx2.c
AVX instructions are like double-wide SSE instructions. They can hold 256 bits (meaning 32 uint8_t), so we require that the width of the input is a multiple of 32. This code achieves a speedup of 72.42x (66.87% of the single CPU peak) over the reference on the 8192x8192 grid for 256 iterations, but because it is so similar to the SSE version we do not include it.
streaming.c
Since we perform 12 operations per byte and an AVX instruction can operate on 32 bytes simultaneously, we might benefit from some memory optimizations. Let’s put a streaming store in the inner loop. A streaming store writes to memory without first reading the value into cache (leaving more room for useful values in the cache). Since we know we do not need to read the value in the new array, this is the perfect operation for us. The last line of our inner loop moves from this:
_mm256_store_si256((__m256i*)(new + y * padded_width + x),
_mm256_or_si256(
_mm256_and_si256(ones, _mm256_cmpeq_epi8(n, threes)),
_mm256_and_si256(alive, _mm256_cmpeq_epi8(n, twos))));To this:
_mm256_stream_si256((__m256i*)(new + y * padded_width + x),
_mm256_or_si256(
_mm256_and_si256(ones, _mm256_cmpeq_epi8(n, threes)),
_mm256_and_si256(alive, _mm256_cmpeq_epi8(n, twos))));And our code now achieves a speedup of 86.44x over the reference on the 8192x8192 grid for 256 iterations. We are now running at 79.82% of the single CPU peak, and I don’t think we’re going to get very many additional speedups. It’s time to go parallel!
omp.c
We have a pretty decent single core utilization, so why don’t we move to multiple cores? OpenMP is a library that makes it easy to distribute loop iterations among threads. Here’s what it looks like:
#pragma omp parallel
{
//To avoid race conditions, each thread keeps their own copy of the
//universe and new pointers
uint8_t *my_universe = universe;
uint8_t *my_new = new;
for (unsigned j = 0; j < IN_GHOST & j + i < iters; j++) {
//We distribute the loop over y, not x, because we want to avoid writing
//to the same cache lines
#pragma omp for
for (unsigned y = (Y_IN_GHOST - Y_OUT_GHOST); y < height + Y_IN_GHOST + Y_OUT_GHOST; y++) {
for (unsigned x = (X_IN_GHOST - X_OUT_GHOST); x + WORD <= width + X_IN_GHOST + X_OUT_GHOST; x += WORD) {
__m256i n;
__m256i alive;
uint8_t *u = my_universe + (y - 1) * padded_width + x - 1;
n = _mm256_lddqu_si256((__m256i*)u);
n = _mm256_add_epi8(_mm256_load_si256((__m256i*)(u + 1)), n);
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
u += padded_width;
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)u), n);
alive = _mm256_load_si256((__m256i*)(u + 1));
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
u += padded_width;
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)u), n);
n = _mm256_add_epi8(_mm256_load_si256((__m256i*)(u + 1)), n);
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
_mm256_stream_si256((__m256i*)(my_new + y * padded_width + x),
_mm256_or_si256(
_mm256_and_si256(ones, _mm256_cmpeq_epi8(n, threes)),
_mm256_and_si256(alive, _mm256_cmpeq_epi8(n, twos))));
}
}
uint8_t *tmp = my_universe;
my_universe = my_new;
my_new = tmp;
}
#pragma omp single
{
//Again to avoid race conditions, a single thread (it doesn't matter
//since all the threads have the same copies of everything) writes their
//copies of the universe and new pointers to the shared copies for the
//next time
universe = my_universe;
new = my_new;
}
}
}Now we are getting the speedups we deserve! This gets a speedup of 375.6x over the reference version on the 8192x8192 grid for 256 iterations, and we are only using 10 of the available 40 processors on this CPU! Keep in mind that we are currently only running at 17.34% of our theoretical peak processing rate!
Our OpenMP code does not scale beyond a single NUMA domain (where communication is cheap). From the following graph, we see that our code gets no real performance gain beyond 10 threads.
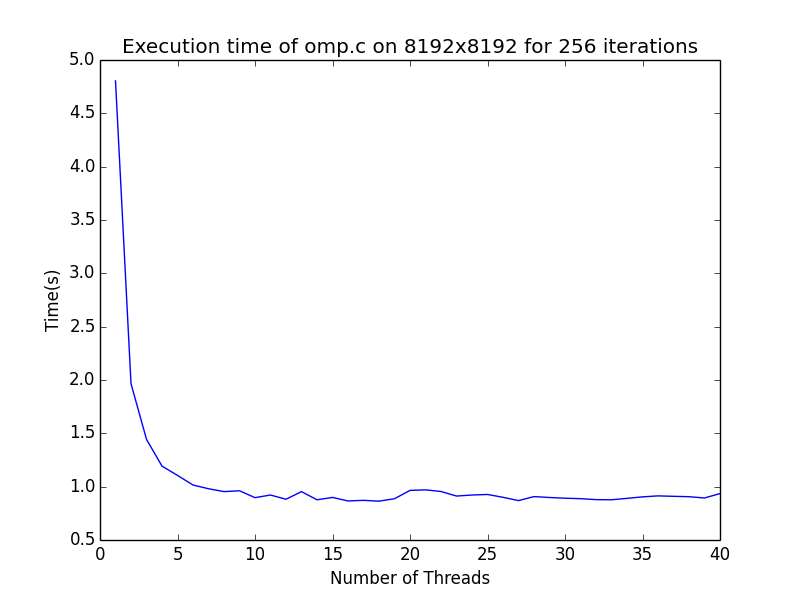
There are a few reasons that this might happen. My guess is that either our processor cannot load memory fast enough to satisfy hungry cpus, or communication is too costly. We should perform a more thorough analysis of why our implementation isn’t scaling, but I like writing code more than I like running it so let’s make a brash decision!
mpi.c
If our code were communication-bound, we might benefit from explicitly managing our communication patterns. We can do this using MPI, to run multiple processes that do not share an address space, and binding processes to physical CPUs. This way, each NUMA domain has a separate MPI task. Our MPI tasks can run OpenMP on their own NUMA domains, and communicate to other explicitly.
Our MPI program makes several simplifications, assuming that the number of processors is a perfect square, that the height is divisible by the square root of the number of processors, and that the width is divisible by the word size times the square root of the number of processes.
Watch out! This MPI code is more that 10 times longer than our reference code. TL;DR: each process is part of a grid, and instead of copying the ghost cells like we did in previous versions, we will send them to our neighbors.
#include <stdlib.h>
#include <stdint.h>
#include <immintrin.h>
#include <math.h>
#include <omp.h>
#include <mpi.h>
#define WORD (256/8)
#define OUT_GHOST 7
#define X_OUT_GHOST (((OUT_GHOST - 1)/WORD + 1) * WORD)
#define Y_OUT_GHOST OUT_GHOST
#define IN_GHOST (OUT_GHOST + 1)
#define X_IN_GHOST ((OUT_GHOST/WORD + 1) * WORD)
#define Y_IN_GHOST IN_GHOST
#define X_IN_GHOST_WORDS (X_IN_GHOST/WORD)
//Here are the tags we will use to distinguish where the data is coming from
//and going to. Notice that the top left corner is sent to the bottom right
//corner of the top left neighbor.
#define TOP_LEFT_SEND 0
#define BOTTOM_RIGHT_RECV 0
#define TOP_SEND 1
#define BOTTOM_RECV 1
#define TOP_RIGHT_SEND 2
#define BOTTOM_LEFT_RECV 2
#define RIGHT_SEND 3
#define LEFT_RECV 3
#define BOTTOM_RIGHT_SEND 4
#define TOP_LEFT_RECV 4
#define BOTTOM_SEND 5
#define TOP_RECV 5
#define BOTTOM_LEFT_SEND 6
#define TOP_RIGHT_RECV 6
#define LEFT_SEND 7
#define RIGHT_RECV 7
void *aligned_malloc(int size) {
char *mem = malloc(sizeof(void*) + size + WORD - 1);
void **ptr = (void**)(((uintptr_t)(mem + sizeof(void*) + WORD - 1)) & ~((uintptr_t)(WORD - 1)));
ptr[-1] = mem;
return ptr;
}
void aligned_free(void *ptr) {
free(((void**)ptr)[-1]);
}
unsigned *life (const unsigned height,
const unsigned width,
const unsigned * const initial,
const unsigned iters) {
int rank;
int size;
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
//We will be arranging our processes in a grid. We are assuming that the
//problem width is divisible by the square root of the number of processors
//times the width of a word, and that the height is divisible by the
//square root of the number of processes, and the number of processes
//is a perfect square
const unsigned side = (int)sqrt((double)size);
const unsigned my_height = height/side;
const unsigned my_width = width/side;
const unsigned my_y = (rank / side);
const unsigned my_x = (rank % side);
const unsigned my_padded_height = my_height + 2 * Y_IN_GHOST;
const unsigned my_padded_width = my_width + 2 * X_IN_GHOST;
const unsigned my_width_words = my_width/WORD;
const unsigned my_padded_width_words = my_padded_width/WORD;
uint8_t *universe = (uint8_t*)aligned_malloc(my_padded_height * my_padded_width);
uint8_t *new = (uint8_t*)aligned_malloc(my_padded_height * my_padded_width);
const __m256i ones = _mm256_set_epi8(1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1);
const __m256i twos = _mm256_slli_epi32(ones, 1);
const __m256i threes = _mm256_or_si256(ones, twos);
//We start by sending the data to all the processes. The data is first
//partitioned into a grid of rectangles (one for each processor).
//Here we first break up the initial data into rectangles.
uint8_t *scatter_buffer_send;
uint8_t *scatter_buffer_recv = (uint8_t*)aligned_malloc(my_height * my_width);
if (rank == 0) {
scatter_buffer_send = (uint8_t*)aligned_malloc(height * width);
for (unsigned their_y = 0; their_y < side; their_y++) {
for (unsigned their_x = 0; their_x < side; their_x++) {
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < my_width; x++) {
scatter_buffer_send[(their_y * side + their_x) * (my_width * my_height) + y * my_width + x] =
initial[(their_y * my_height + y) * width + their_x * my_width + x];
}
}
}
}
}
MPI_Scatter((const void*)scatter_buffer_send,
my_height * my_width,
MPI_UNSIGNED_CHAR,
(void*)scatter_buffer_recv,
my_height * my_width,
MPI_UNSIGNED_CHAR,
0,
MPI_COMM_WORLD);
//Now that the data has been scattered, we copy our personal rectangle into
//our local universe.
for (unsigned y = Y_IN_GHOST; y < Y_IN_GHOST + my_height; y++) {
for (unsigned x = X_IN_GHOST; x < X_IN_GHOST + my_width; x++) {
universe[(y * my_padded_width) + x] = scatter_buffer_recv[(y - Y_IN_GHOST) * my_width + x - X_IN_GHOST];
}
}
//There's a bunch of send buffers aren't there?
__m256i *ghost_buffer_top_left_send = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_top_send = (__m256i*)aligned_malloc( my_width * Y_IN_GHOST);
__m256i *ghost_buffer_top_right_send = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_right_send = (__m256i*)aligned_malloc(X_IN_GHOST * my_height );
__m256i *ghost_buffer_bottom_right_send = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_bottom_send = (__m256i*)aligned_malloc( my_width * Y_IN_GHOST);
__m256i *ghost_buffer_bottom_left_send = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_left_send = (__m256i*)aligned_malloc(X_IN_GHOST * my_height );
__m256i *ghost_buffer_bottom_right_recv = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_bottom_recv = (__m256i*)aligned_malloc( my_width * Y_IN_GHOST);
__m256i *ghost_buffer_bottom_left_recv = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_left_recv = (__m256i*)aligned_malloc(X_IN_GHOST * my_height );
__m256i *ghost_buffer_top_left_recv = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_top_recv = (__m256i*)aligned_malloc( my_width * Y_IN_GHOST);
__m256i *ghost_buffer_top_right_recv = (__m256i*)aligned_malloc(X_IN_GHOST * Y_IN_GHOST);
__m256i *ghost_buffer_right_recv = (__m256i*)aligned_malloc(X_IN_GHOST * my_height );
MPI_Request top_left_req;
MPI_Request top_req;
MPI_Request top_right_req;
MPI_Request right_req;
MPI_Request bottom_right_req;
MPI_Request bottom_req;
MPI_Request bottom_left_req;
MPI_Request left_req;
for (unsigned i = 0; i < iters; i+= IN_GHOST) {
__m256i *universe_words = (__m256i*)universe;
//Here are all of the sends to our neighbors in every cardinal direction.
//The sends are nonblocking, so that we can move right on to the next send
//without waiting for our neighbors to receive.
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_top_left_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (Y_IN_GHOST + y) * my_padded_width_words + X_IN_GHOST_WORDS + x));
}
}
MPI_Isend(ghost_buffer_top_left_send,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + ((my_x + side - 1) % side),
TOP_LEFT_SEND,
MPI_COMM_WORLD,
&top_left_req);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < my_width_words; x++) {
_mm256_store_si256(ghost_buffer_top_send + y * my_width_words + x,
_mm256_load_si256(universe_words + (Y_IN_GHOST + y) * my_padded_width_words + X_IN_GHOST_WORDS + x));
}
}
MPI_Isend(ghost_buffer_top_send,
my_width * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + my_x,
TOP_SEND,
MPI_COMM_WORLD,
&top_req);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_top_right_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (y + Y_IN_GHOST) * my_padded_width_words + x + my_width_words));
}
}
MPI_Isend(ghost_buffer_top_right_send,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + ((my_x + 1) % side),
TOP_RIGHT_SEND,
MPI_COMM_WORLD,
&top_right_req);
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_right_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (y + Y_IN_GHOST) * my_padded_width_words + x + my_width_words));
}
}
MPI_Isend(ghost_buffer_right_send,
X_IN_GHOST * my_height,
MPI_UNSIGNED_CHAR,
my_y * side + ((my_x + 1) % side),
RIGHT_SEND,
MPI_COMM_WORLD,
&right_req);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_bottom_right_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (y + my_height) * my_padded_width_words + x + my_width_words));
}
}
MPI_Isend(ghost_buffer_bottom_right_send,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + ((my_x + 1) % side),
BOTTOM_RIGHT_SEND,
MPI_COMM_WORLD,
&bottom_right_req);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < my_width_words; x++) {
_mm256_store_si256(ghost_buffer_bottom_send + y * my_width_words + x,
_mm256_load_si256(universe_words + (y + my_height) * my_padded_width_words + x + X_IN_GHOST_WORDS));
}
}
MPI_Isend(ghost_buffer_bottom_send,
my_width * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + my_x,
BOTTOM_SEND,
MPI_COMM_WORLD,
&bottom_req);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_bottom_left_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (y + my_height) * my_padded_width_words + x + X_IN_GHOST_WORDS));
}
}
MPI_Isend(ghost_buffer_bottom_left_send,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + ((my_x + side - 1) % side),
BOTTOM_LEFT_SEND,
MPI_COMM_WORLD,
&bottom_left_req);
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(ghost_buffer_left_send + y * X_IN_GHOST_WORDS + x,
_mm256_load_si256(universe_words + (y + Y_IN_GHOST) * my_padded_width_words + x + X_IN_GHOST_WORDS));
}
}
MPI_Isend(ghost_buffer_left_send,
X_IN_GHOST * my_height,
MPI_UNSIGNED_CHAR,
my_y * side + ((my_x + side - 1) % side),
LEFT_SEND,
MPI_COMM_WORLD,
&left_req);
//Now we receive ghost zones from all of our neighbors. Since we need to
//process our received data immediately, the received data is blocking.
MPI_Recv((void*)ghost_buffer_bottom_right_recv,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + ((my_x + 1) % side),
BOTTOM_RIGHT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + (y + Y_IN_GHOST + my_height) * my_padded_width_words + x + X_IN_GHOST_WORDS + my_width_words,
_mm256_load_si256(ghost_buffer_bottom_right_recv + y * X_IN_GHOST_WORDS + x));
}
}
MPI_Recv((void*)ghost_buffer_bottom_recv,
my_width * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + my_x,
BOTTOM_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < my_width_words; x++) {
_mm256_store_si256(universe_words + (y + Y_IN_GHOST + my_height) * my_padded_width_words + x + X_IN_GHOST_WORDS,
_mm256_load_si256(ghost_buffer_bottom_recv + y * my_width_words + x));
}
}
MPI_Recv((void*)ghost_buffer_bottom_left_recv,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + 1) % side) * side + ((my_x + side - 1) % side),
BOTTOM_LEFT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + (y + Y_IN_GHOST + my_height) * my_padded_width_words + x,
_mm256_load_si256(ghost_buffer_bottom_left_recv + y * X_IN_GHOST_WORDS + x));
}
}
MPI_Recv((void*)ghost_buffer_left_recv,
X_IN_GHOST * my_height,
MPI_UNSIGNED_CHAR,
my_y * side + ((my_x + side - 1) % side),
LEFT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + (y + Y_IN_GHOST) * my_padded_width_words + x,
_mm256_load_si256(ghost_buffer_left_recv + y * X_IN_GHOST_WORDS + x));
}
}
MPI_Recv((void*)ghost_buffer_top_left_recv,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + ((my_x + side - 1) % side),
TOP_LEFT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + y * my_padded_width_words + x,
_mm256_load_si256(ghost_buffer_top_left_recv + y * X_IN_GHOST_WORDS + x));
}
}
MPI_Recv((void*)ghost_buffer_top_recv,
my_width * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + my_x,
TOP_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < my_width_words; x++) {
_mm256_store_si256(universe_words + y * my_padded_width_words + x + X_IN_GHOST_WORDS,
_mm256_load_si256(ghost_buffer_top_recv + y * my_width_words + x));
}
}
MPI_Recv((void*)ghost_buffer_top_right_recv,
X_IN_GHOST * Y_IN_GHOST,
MPI_UNSIGNED_CHAR,
((my_y + side - 1) % side) * side + ((my_x + 1) % side),
TOP_RIGHT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < Y_IN_GHOST; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + y * my_padded_width_words + x + X_IN_GHOST_WORDS + my_width_words,
_mm256_load_si256(ghost_buffer_top_right_recv + y * X_IN_GHOST_WORDS + x));
}
}
MPI_Recv((void*)ghost_buffer_right_recv,
X_IN_GHOST * my_height,
MPI_UNSIGNED_CHAR,
my_y * side + ((my_x + 1) % side),
RIGHT_RECV,
MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < X_IN_GHOST_WORDS; x++) {
_mm256_store_si256(universe_words + (y + Y_IN_GHOST) * my_padded_width_words + x + X_IN_GHOST_WORDS + my_width_words,
_mm256_load_si256(ghost_buffer_right_recv + y * X_IN_GHOST_WORDS + x));
}
}
//The inner loop is the same.
#pragma omp parallel
{
uint8_t *my_universe = universe;
uint8_t *my_new = new;
for (unsigned j = 0; j < IN_GHOST & j + i < iters; j++) {
#pragma omp for
for (unsigned y = (Y_IN_GHOST - Y_OUT_GHOST); y < my_height + Y_IN_GHOST + Y_OUT_GHOST; y++) {
for (unsigned x = (X_IN_GHOST - X_OUT_GHOST); x + WORD <= my_width + X_IN_GHOST + X_OUT_GHOST; x += WORD) {
__m256i n;
__m256i alive;
uint8_t *u = my_universe + (y - 1) * my_padded_width + x - 1;
n = _mm256_lddqu_si256((__m256i*)u);
n = _mm256_add_epi8(_mm256_load_si256((__m256i*)(u + 1)), n);
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
u += my_padded_width;
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)u), n);
alive = _mm256_load_si256((__m256i*)(u + 1));
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
u += my_padded_width;
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)u), n);
n = _mm256_add_epi8(_mm256_load_si256((__m256i*)(u + 1)), n);
n = _mm256_add_epi8(_mm256_lddqu_si256((__m256i*)(u + 2)), n);
_mm256_stream_si256((__m256i*)(my_new + y * my_padded_width + x),
_mm256_or_si256(
_mm256_and_si256(ones, _mm256_cmpeq_epi8(n, threes)),
_mm256_and_si256(alive, _mm256_cmpeq_epi8(n, twos))));
}
}
uint8_t *tmp = my_universe;
my_universe = my_new;
my_new = tmp;
}
#pragma omp single
{
universe = my_universe;
new = my_new;
}
}
//Before we start another iteration and start sending again, let's make sure
//that everyone has received our messages.
MPI_Wait(&top_left_req, MPI_STATUS_IGNORE);
MPI_Wait(&top_req, MPI_STATUS_IGNORE);
MPI_Wait(&top_right_req, MPI_STATUS_IGNORE);
MPI_Wait(&right_req, MPI_STATUS_IGNORE);
MPI_Wait(&bottom_right_req, MPI_STATUS_IGNORE);
MPI_Wait(&bottom_req, MPI_STATUS_IGNORE);
MPI_Wait(&bottom_left_req, MPI_STATUS_IGNORE);
MPI_Wait(&left_req, MPI_STATUS_IGNORE);
}
unsigned *out = NULL;
//This part is very similar to the Scatter. We now have all of the final
//configurations, and need to send them to the master process so that we
//can return a matrix.
for (unsigned y = Y_IN_GHOST; y < Y_IN_GHOST + my_height; y++) {
for (unsigned x = X_IN_GHOST; x < X_IN_GHOST + my_width; x++) {
scatter_buffer_recv[(y - Y_IN_GHOST) * my_width + x - X_IN_GHOST] = universe[y * my_padded_width + x];
}
}
MPI_Gather((const void*)scatter_buffer_recv,
my_height * my_width,
MPI_UNSIGNED_CHAR,
(void*)scatter_buffer_send,
my_height * my_width,
MPI_UNSIGNED_CHAR,
0,
MPI_COMM_WORLD);
if (rank == 0) {
out = (unsigned*)malloc(sizeof(unsigned) * height * width);
for (unsigned their_y = 0; their_y < side; their_y++) {
for (unsigned their_x = 0; their_x < side; their_x++) {
for (unsigned y = 0; y < my_height; y++) {
for (unsigned x = 0; x < my_width; x++) {
out[(their_y * my_height + y) * width + their_x * my_width + x] =
scatter_buffer_send[(their_y * side + their_x) * (my_width * my_height) + y * my_width + x];
}
}
}
}
}
aligned_free(new);
aligned_free(universe);
aligned_free(ghost_buffer_top_left_send);
aligned_free(ghost_buffer_top_send);
aligned_free(ghost_buffer_top_right_send);
aligned_free(ghost_buffer_right_send);
aligned_free(ghost_buffer_bottom_right_send);
aligned_free(ghost_buffer_bottom_send);
aligned_free(ghost_buffer_bottom_left_send);
aligned_free(ghost_buffer_left_send);
aligned_free(ghost_buffer_top_left_recv);
aligned_free(ghost_buffer_top_recv);
aligned_free(ghost_buffer_top_right_recv);
aligned_free(ghost_buffer_right_recv);
aligned_free(ghost_buffer_bottom_right_recv);
aligned_free(ghost_buffer_bottom_recv);
aligned_free(ghost_buffer_bottom_left_recv);
aligned_free(ghost_buffer_left_recv);
if (rank == 0) {
aligned_free(scatter_buffer_send);
}
aligned_free(scatter_buffer_recv);
return out;
}This implementation runs our 8192x8192 problem for 256 iterations in 0.58 seconds, a speedup of 462.30x over the reference code. We did gain some performance by explicitly managing our memory, but it appears that we have not achieved full utilization of our single processor.
You may be wondering why mpi.c is faster than the omp.c. After all, omp.c performs as well at 10 threads as it does at 40 threads, and mpi.c has a lot of extra copying into buffers, etc. I suspect that because the MPI code explicitly manages communication, passing only the ghost zones to its neighbors once every couple of iterations, mpi.c spends less time in communication. The OpenMP version of the code leaves the communication to the cache, which doesn’t know or care about our delicate ghost zones. By keeping two MPI processes on each NUMA node with 10 OpenMP threads each, we can explicitly manage communication between NUMA nodes.
Perhaps an interested reader can help explain to me why the application does not scale beyond 10 or so CPUs. My hypothesis is that we are memory-bound at some level of the cache, meaning that most of the processors are waiting to load life cells from memory instead of staying busy computing lice cells.
A benefit of rewriting using MPI is that we can now run our program on an arbitrary number of nodes networked together. Who cares about single processor performance when you can have 400 processors? Future work!
Conclusion
Here is a table showing the various times, speedups, and percentages of peak for each code:
| Code | Time (seconds) | Speedup (over reference.c) | % of peak |
|---|---|---|---|
| reference.c | 268.33 | 1.00 | 0.05 |
| simple.c | 208.35 | 1.29 | 0.06 |
| padded.c | 51.59 | 5.20 | 0.24 |
| sse2.c | 4.62 | 58.06 | 2.68 |
| avx2.c | 3.71 | 72.42 | 3.34 |
| streaming.c | 3.10 | 86.44 | 3.99 |
| omp.c | 0.71 | 375.60 | 17.34 |
| mpi.c | 0.58 | 462.30 | 21.34 |
Hopefully you had as much fun reading this code as I did writing it. This writeup is heavy on code and light on analysis, but I hope you enjoyed following me on my journey through life.
Copyright
Copyright (c) 2016, Los Alamos National Security, LLC
All rights reserved.
Copyright 2016. Los Alamos National Security, LLC. This software was produced under U.S. Government contract DE-AC52-06NA25396 for Los Alamos National Laboratory (LANL), which is operated by Los Alamos National Security, LLC for the U.S. Department of Energy. The U.S. Government has rights to use, reproduce, and distribute this software. NEITHER THE GOVERNMENT NOR LOS ALAMOS NATIONAL SECURITY, LLC MAKES ANY WARRANTY, EXPRESS OR IMPLIED, OR ASSUMES ANY LIABILITY FOR THE USE OF THIS SOFTWARE. If software is modified to produce derivative works, such modified software should be clearly marked, so as not to confuse it with the version available from LANL.
Additionally, redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
- Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
- Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
- Neither the name of Los Alamos National Security, LLC, Los Alamos National Laboratory, LANL, the U.S. Government, nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY LOS ALAMOS NATIONAL SECURITY, LLC AND CONTRIBUTORS “AS IS” AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL LOS ALAMOS NATIONAL SECURITY, LLC OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
